浮点数
在计算机科学中，浮点（英语：floating point，缩写为FP）是一种对于实数的近似值数值表现法，由一个有效数字（即尾数）加上幂数来表示，通常是乘以某个基数的整数次指数得到。以这种表示法表示的数值，称为浮点数（floating-point number）。利用浮点进行运算，称为浮点计算，这种运算通常伴随着因为无法精确表示而进行的近似或舍入。
这种表示方法类似于基数为10的科学记数法，在计算机上，通常使用2为基数的幂数来表示。一个浮点数a由两个数m和e来表示：a = m × b^e。在任意一个这样的系统中，我们选择一个基数b（记数系统的基）和精度p（即使用多少位来存储）。m（即尾数）是形如±d.ddd…ddd的p位数（每一位是一个介于0到b-1之间的整数，包括0和b-1）。如果m的第一位是非0整数，m称作正规化的。有一些描述使用一个单独的符号位（s 代表+或者-）来表示正负，这样m必须是正的。e是指数。
这种表示法的设计，来自于对于值的表现范围，与精密度之间的取舍：可以在某个固定长度的存储空间内表示出某个实数的近似值。例如，一个指数范围为±4的4位十进制浮点数可以用来表示43210，4.321或0.0004321，但是没有足够的精度来表示432.123和43212.3（必须近似为432.1和43210）。当然，实际使用的位数通常远大于4。
此外，浮点数表示法通常还包括一些特别的数值：+∞和−∞（正负无穷大）以及NaN（’Not a Number’）。无穷大用于数太大而无法表示的时候，NaN则指示非法操作或者无法定义的结果。
其中，无穷大，可表示为inf，在内存中的值是阶码为全1，尾数全0。而NaN在内存中的值则是阶码全1，尾数不全0。
计算机的浮点数
浮点指的是带有小数的数值，浮点运算即是小数的四则运算，常用来测量电脑运算速度。大部分计算机采用二进制（b=2）的表示方法。位（bit）是衡量浮点数所需存储空间的单位，通常为32位或64位，分别被叫作单精度和双精度。有一些计算机提供更大的浮点数，例如英特尔公司的浮点运算单元Intel8087协处理器（以及其被集成进x86处理器中的后代产品）提供80位长的浮点数，用于存储浮点运算的中间结果。还有一些系统提供128位的浮点数（通常用软件实现）。
浮点数的标准
在电脑使用的浮点数被电气电子工程师协会（IEEE）规范化为IEEE 754。
举例
π的值可以表示为π = 3.1415926…10（十进制）。当在一个支持17位尾数的计算机中表示时，它会变为0.11001001000011111 × 2^2。
准确性
由于浮点数不能表达所有实数，浮点运算与相应的数学运算有所差异，有时此差异极为显著。
比如，二进制浮点数不能表达0.1和0.01，0.1的平方既不是准确的0.01，也不是最接近0.01的可表达的数。单精度（24比特）浮点数表示0.1的结果为
即
0.100000001490116119384765625
此数的平方是
0.010000000298023226097399174250313080847263336181640625
但最接近0.01的可表达的数是
0.009999999776482582092285156250
浮点数也不能表达圆周率
的计算结果为16331239353195370.0，如果用单精度浮点数，则结果为−22877332.0。同样的，
由于浮点数计算过程中丢失了精度，浮点运算的性质与数学运算有所不同。浮点加法和乘法不匹配结合律和分配律。
单精度浮点数
单精度浮点数格式是一种计算机数据格式，在计算机存储器中占用4个字节（32 bits），利用“浮点”（浮动小数点）的方法，可以表示一个范围很大的数值。
在IEEE 754-2008的定义中，32-bit base 2格式被正式称为binary32格式。这种格式在IEEE 754-1985被定义为single，即单精度。需要注意的是，在更早的一些计算机系统中，也存在着其他4字节的浮点数格式。
定义
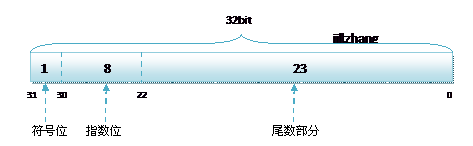
第1位表示正负，中间8位表示指数，后23位储存有效数位（有效数位是24位）。
正负号0代表正，1代表负。
指数可以是二补码；或0到255，前半代表负，127代表零，后半代表正。
有效数位最左手边的1并不会储存，因为它一定存在（二进制的第一个有效数字必定是1）。换言之，有效数位是24位，实际储存23位。
双精度浮点数
双精度浮点数（double）是计算机使用的一种数据类型。比起单精度浮点数，双精度浮点数(double)使用 64 位（8字节） 来存储一个浮点数。 它可以表示十进制的15或16位有效数字，其可以表示的数字的绝对值范围大约是
格式
sign bit(符号): 用来表示正负号
exponent(指数): 用来表示次方数
mantissa(尾数): 用来表示精确度
符号
0代表数值为正，1代表数值为负。
指数
类比整型使用所有位为 0 的数字表示数值“0”，双精度浮点数表示 0 时指数部分也为 0。若如此，便可能产生冲突：比如全 0 的数字可能表示“0”，也可能表示
其他：代表 2 的（exponent-0x3ff）次方。
尾数
在二进制的“科学记号”，数字被表示为：
为了最大限度提高精确度，可以要求尾数规格化，把尾数处理到大于等于1而小于2的区间内，便可省去前导的“1”。例如：
于是，可得以下形式：
小结
根据以上的叙述，一个双精度浮点数所代表的数值为：
例子
|
|
计算机基础——信息的表示与存储
浮点数在计算机中存储方式
不论是float还是double在存储方式上都是遵从IEEE的规范的，float遵从的是IEEE R32.24 ,而double 遵从的是R64.53。
- 符号位(Sign) : 0代表正，1代表为负
- 指数位（Exponent）:用于存储科学计数法中的指数数据，并且采用移位存储
尾数部分（Mantissa）：尾数部分
其中float的存储方式如下图所示：
而双精度的存储方式为:
R32.24和R64.53的存储方式都是用科学计数法来存储数据的，比如8.25用十进制的科学计数法表示就为:8.25
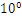,而120.5可以表示为:1.205
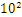,这些小学的知识就不用多说了吧。而我们傻蛋计算机根本不认识十进制的数据，他只认识0，1，所以在计算机存储中，首先要将上面的数更改为二进制的科学计数法表示，8.25用二进制表示可表示为1000.01,我靠，不会连这都不会转换吧?那我估计要没辙了。120.5用二进制表示为：1110110.1用二进制的科学计数法表示1000.01可以表示为1.0001
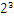,1110110.1可以表示为1.1101101
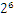,任何一个数都的科学计数法表示都为1.xxx*
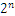,尾数部分就可以表示为xxxx,第一位都是1嘛，干嘛还要表示呀？可以将小数点前面的1省略，所以23bit的尾数部分，可以表示的精度却变成了24bit，道理就是在这里，那24bit能精确到小数点后几位呢，我们知道9的二进制表示为1001，所以4bit能精确十进制中的1位小数点，24bit就能使float能精确到小数点后6位，而对于指数部分，因为指数可正可负，8位的指数位能表示的指数范围就应该为:-127-128了，所以指数部分的存储采用移位存储，存储的数据为元数据+127，下面就看看8.25和120.5在内存中真正的存储方式。首先看下8.25，用二进制的科学计数法表示为:1.0001*
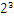
按照上面的存储方式，符号位为:0，表示为正，指数位为:3+127=130 ,位数部分为,故8.25的存储方式如下图所示: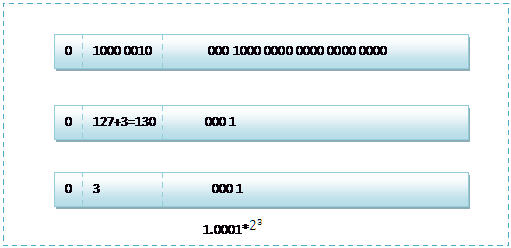
而单精度浮点数120.5的存储方式如下图所示:
1.1101101*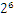
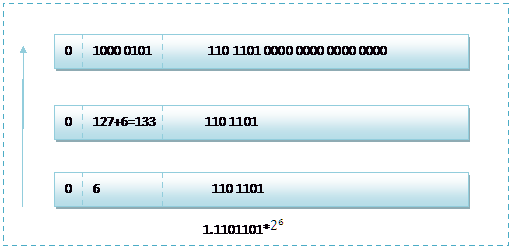
那么如果给出内存中一段数据，并且告诉你是单精度存储的话，你如何知道该数据的十进制数值呢？其实就是对上面的反推过程，比如给出如下内存数据：0100001011101101000000000000，首先我们现将该数据分段，0 10000 0101 110 1101 0000 0000 0000 0000，在内存中的存储就为下图所示：
http://images.cnblogs.com/cnblogs_com/jillzhang/WindowsLiveWriter/float_A919/clip_image001_1.gif
根据我们的计算方式，可以计算出，这样一组数据表示为:1.1101101*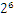=120.5
而双精度浮点数的存储和单精度的存储大同小异，不同的是指数部分和尾数部分的位数。所以这里不再详细的介绍双精度的存储方式了，只将120.5的最后存储方式图给出，大家可以仔细想想为何是这样子的
下面我就这个基础知识点来解决一个我们的一个疑惑，请看下面一段程序，注意观察输出结果
float f = 2.2f;
double d = (double)f;
Console.WriteLine(d.ToString("0.0000000000000"));
f = 2.25f;
d = (double)f;
Console.WriteLine(d.ToString("0.0000000000000"));
可能输出的结果让大家疑惑不解，单精度的2.2转换为双精度后，精确到小数点后13位后变为了2.2000000476837，而单精度的2.25转换为双精度后，变为了2.2500000000000，为何2.2在转换后的数值更改了而2.25却没有更改呢？很奇怪吧？其实通过上面关于两种存储结果的介绍，我们已经大概能找到答案。首先我们看看2.25的单精度存储方式，很简单 0 1000 0001 001 0000 0000 0000 0000 0000,而2.25的双精度表示为:0 100 0000 0001 0010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,这样2.25在进行强制转换的时候，数值是不会变的，而我们再看看2.2呢，2.2用科学计数法表示应该为：将十进制的小数转换为二进制的小数的方法为将小数2，取整数部分，所以0.282=0.4，所以二进制小数第一位为0.4的整数部分0，0.4×2=0.8，第二位为0,0.82=1.6,第三位为1，0.6×2 = 1.2，第四位为1，0.2*2=0.4，第五位为0，这样永远也不可能乘到=1.0，得到的二进制是一个无限循环的排列 00110011001100110011… ,对于单精度数据来说，尾数只能表示24bit的精度，所以2.2的float存储为:
但是这样存储方式，换算成十进制的值，却不会是2.2的，应为十进制在转换为二进制的时候可能会不准确，如2.2，而double类型的数据也存在同样的问题，所以在浮点数表示中会产生些许的误差，在单精度转换为双精度的时候，也会存在误差的问题，对于能够用二进制表示的十进制数据，如2.25，这个误差就会不存在，所以会出现上面比较奇怪的输出结果。
本文属作者原创，只发布在博客园，希望大家在转载的时候，注明出处和作者，谢谢。
注：本文在写作过程中，参照了如下资料：
http://blog.csdn.net/ganxingming/archive/2006/12/19/1449526.aspx
C语言中float,double类型,在内存中的结构(存储方式)
C语言中float,double类型,在内存中的结构(存储方式)
从存储结构和算法上来讲，double和float是一样的，不一样的地方仅仅是float是32位的，double是64位的，所以double能存储更高的精度。
任何数据在内存中都是以二进制（0或1）顺序存储的，每一个1或0被称为1位，而在x86CPU上一个字节是8位。比如一个16位（2 字节）的short int型变量的值是1000，那么它的二进制表达就是：00000011 11101000。由于Intel CPU的架构原因，它是按字节倒 序存储的，那么就因该是这样：11101000 00000011，这就是定点数1000在内存中的结构。
目前C/C++编译器标准都遵照IEEE制定的浮点数表示法来进行float,double运算。
这种结构是一种科学计数法，用符号、指数和 尾数来表示，底数定为2——即把一个浮点数表示为尾数乘以2的指数次方再添上符号。
下面是具体的规格：
类型 符号位 阶码 尾数 长度
float 1 8 23 32
double 1 11 52 64
临时数 1 15 64 80
由于通常C编译器默认浮点数是double型的，下面以double为例： 共计64位，折合8字节。
由最高到最低位分别是第63、62、61、……、0位： 最高位63位是符号位，1表示该数为负，0正； 62-52位，一共11位是指数位； 51-0位，一共52位是尾数位。
按照IEEE浮点数表示法，下面将把double型浮点数38414.4转换为十六进制代码。
把整数部和小数部分开处理:整数部直接化十六进制：960E。小数的处理: 0.4=0.50+0.251+0.1251+0.06250+…… 实际上这永远算不完！这就是著名的浮点数精度问题。所以直到加上前面的整数部分算够53位就行了（隐藏位技术：最高位的1 不写入内存）。
如果你够耐心，手工算到53位那么因该是：38414.4(10)=1001011000001110.0110101010101010101010101010101010101(2)
科学记数法为：1.001……乘以2的15次方。指数为15！ 于是来看阶码，一共11位，可以表示范围是-1024 ~ 1023。因为指数可以为负，为了便于计算，规定都先加上1023，在这里， 15+1023=1038。
二进制表示为：100 00001110 符号位：正—— 0 ！ 合在一起（尾数二进制最高位的1不要）： 01000000 11100010 11000001 11001101 01010101 01010101 01010101 01010101 按字节倒序存储的十六进制数就是： 55 55 55 55 CD C1 E2 40。
参考资料
浮点数
单精度浮点数
双精度浮点数
计算机基础——信息的表示与存储
浮点数在计算机中存储方式
C语言中float,double类型,在内存中的结构(存储方式)